El diseño de engranajes parece sencillo hasta que uno se enfrenta a la realidad de los parámetros interdependientes. Un simple cambio de módulo afecta al diámetro, la resistencia y el coste. Si se ajusta el ángulo de presión, se cambia la resistencia de los dientes por un funcionamiento suave.
Los parámetros de los engranajes son las especificaciones dimensionales y geométricas que definen el tamaño, la forma y las características de rendimiento de un engranaje. Incluyen el módulo, el número de dientes, el ángulo de presión, el diámetro de paso y la anchura de la cara, que en conjunto determinan cómo engranan los engranajes, transmiten la potencia y encajan en los sistemas mecánicos.
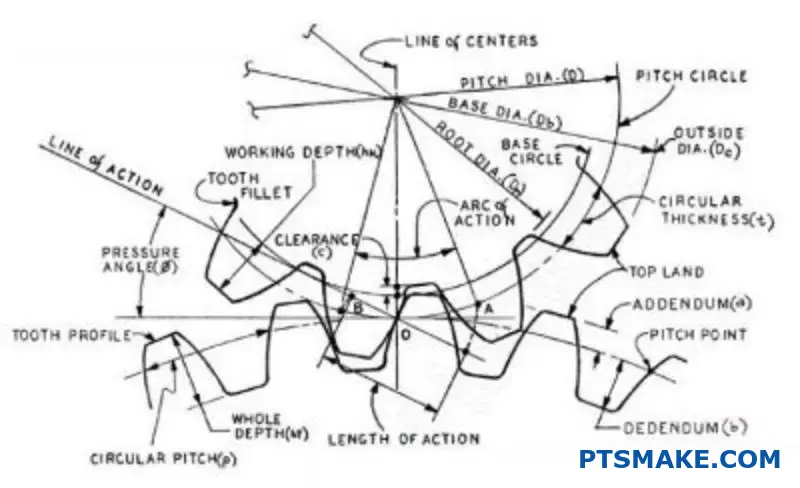
Dominar estos parámetros significa comprender sus relaciones y compensaciones. Le guiaré a través del propósito práctico de cada parámetro, le mostraré cómo interactúan y compartiré los marcos de toma de decisiones que le ayudarán a optimizar los diseños de engranajes para sus aplicaciones específicas.
¿Cuál es el papel fundamental del módulo (o paso diametral)?
El módulo es la unidad fundamental del tamaño de un engranaje. Es como el ADN del engranaje. Define directamente el tamaño de los dientes del engranaje.
Este único valor es crucial. Un módulo más grande significa dientes más grandes y fuertes. Un módulo más pequeño da como resultado dientes más finos y precisos.
Por qué el módulo es lo primero
En el diseño de cualquier nuevo engranaje, el módulo es el punto de partida. Dicta las proporciones generales y la fuerza del engranaje. Muchos clientes preguntan: "¿Cuáles son los parámetros de un engranaje? Yo siempre les digo que empiecen por aquí.
| Módulo (m) | Característica del diente | Ejemplo de aplicación |
|---|---|---|
| 1 | Fino | Pequeña robótica, impresoras |
| 3 | Medio | Transmisión de automóviles |
| 5 | Grueso | Maquinaria pesada |
Esta elección inicial equilibra la necesidad de transmisión de potencia con la precisión requerida para la aplicación. Sienta las bases para todos los demás cálculos.

El módulo como norma universal
El módulo no es sólo un número. Es un sistema que normaliza la fabricación de engranajes. Simplifica todo el proceso de diseño y engrane.
Dos engranajes con el mismo módulo engranarán perfectamente. Esto es así aunque tengan un número diferente de dientes. Esta interoperabilidad es fundamental en el diseño mecánico.
Esta normalización es un principio básico que seguimos en PTSMAKE. Garantiza que los componentes que mecanizamos para distintos clientes funcionen juntos a la perfección.
Módulo métrico frente a paso diametral imperial
Mientras que el sistema métrico utiliza el módulo, el sistema imperial utiliza el Paso Diametral (DP). Sirven para lo mismo, pero están inversamente relacionados.
El módulo es el diámetro de paso dividido por el número de dientes. Un número de módulo mayor significa un diente mayor. El número de dientes y el módulo determinan el tamaño de la rueda dentada. diámetro del círculo primitivo1.
El paso diametral es el número de dientes por pulgada de diámetro de paso. Un número DP mayor significa un diente más pequeño. Puede resultar confuso, pero el objetivo es el mismo: estandarizar el tamaño del diente para un engrane correcto.
| Sistema | Parámetros clave | Relación con el tamaño de los dientes |
|---|---|---|
| Métrica | Módulo (m) | Más grande m = Diente más grande |
| Imperial | Paso diametral (DP) | Más grande DP = Diente más pequeño |
Comprender ambas es esencial para los proyectos de fabricación global. Garantiza que cumplimos las especificaciones exactas, ya sean de un cliente europeo o estadounidense.
El módulo, o paso diametral, es el parámetro fundamental en el diseño de engranajes. Establece el tamaño de los dientes, dicta las dimensiones generales del engranaje y garantiza la compatibilidad entre engranajes, por lo que es la primera y más crítica decisión de diseño.
¿Qué representa físicamente el número de dientes (z)?
El número de dientes (z) es algo más que un simple recuento. Es un parámetro de diseño fundamental. Junto con el módulo (m), define directamente el tamaño físico de un engranaje.
En concreto, estos dos valores determinan el diámetro del círculo primitivo (d). La fórmula es sencilla: d = m × z. Esto significa que el tamaño de un engranaje no es arbitrario. Es el resultado directo de estas especificaciones básicas. Esta relación es crucial para el diseño de engranajes.
| Número de dientes (z) | Módulo (m) | Diámetro del círculo primitivo (d) |
|---|---|---|
| 20 | 2 | 40 mm |
| 40 | 2 | 80 mm |
| 20 | 3 | 60 mm |
Esta tabla muestra cómo afecta la modificación del número de dientes o del módulo al diámetro total de la rueda dentada.

El papel principal en la definición de la relación de transmisión
La función más importante del número de dientes es establecer la relación de transmisión. Esta relación es la relación entre el número de dientes de dos engranajes. Dicta la velocidad de salida y el par de un sistema de engranajes.
Por ejemplo, si una rueda motriz de 20 dientes (z1) engrana con una rueda conducida de 40 dientes (z2), la relación de transmisión es de 2:1. La velocidad de salida se reduce a la mitad, pero el par se duplica. La velocidad de salida se reducirá a la mitad, pero el par se duplicará. Este principio es fundamental en la transmisión mecánica de potencia.
En nuestro trabajo en PTSMAKE, ayudamos con frecuencia a los clientes a seleccionar los parámetros de engranaje adecuados para lograr un control preciso del movimiento en proyectos de robótica y automatización.
Impacto en la suavidad de la transmisión
El número de dientes también influye significativamente en la suavidad de funcionamiento de un engranaje. Por lo general, cuantos más dientes, más suave y silenciosa es la transmisión.
Esto ocurre porque un mayor número de dientes aumenta la compromiso de engrane2 entre los engranajes. Con más dientes en contacto en un momento dado, la carga se distribuye más uniformemente. Esto reduce las vibraciones y el ruido.
Dientes pequeños frente a dientes grandes
- Menos dientes y más grandes: Puede soportar cargas más elevadas, pero puede producir más ruido y vibraciones.
- Más dientes, más pequeños: Ofrecen un funcionamiento más suave y silencioso, pero pueden tener una menor capacidad de carga por diente.
La elección del número de dientes adecuado implica un equilibrio entre resistencia, velocidad, par y suavidad de funcionamiento para la aplicación específica.
El número de dientes, combinado con el módulo, establece el tamaño del engranaje. Es el factor principal para determinar la relación de transmisión, que controla la velocidad y el par. También influye en la suavidad y el nivel de ruido del funcionamiento del engranaje.
¿Qué es el ángulo de presión (α) y cuál es su función principal?
El ángulo de presión (α) es un factor clave en el diseño de engranajes. Define el ángulo de transmisión de la fuerza entre los dientes del engranaje. Este ángulo influye directamente en el rendimiento y la resistencia del engranaje.
Entender qué parámetros del engranaje son importantes es vital. El ángulo de presión es uno de los más importantes. La mayoría de los engranajes modernos utilizan un estándar de 20°. Esto ofrece un gran equilibrio entre resistencia y eficacia.
El compromiso básico
El ángulo de presión de un engranaje crea un equilibrio fundamental. Es un equilibrio entre la resistencia a la flexión y la tensión de contacto en los dientes.
| Ángulo de presión | Resistencia a la flexión | Tensión de contacto y carga de apoyo |
|---|---|---|
| Inferior (por ejemplo, 14,5°) | Base dental más débil | Baja |
| Superior (por ejemplo, 20°, 25°) | Base dental más fuerte | Más alto |
La elección del ángulo correcto es crucial para la aplicación prevista y la vida útil del engranaje.

Una inmersión más profunda: Normas y consecuencias
El ángulo de presión es el ángulo entre la línea de fuerza y una línea tangente al círculo primitivo. La propia fuerza se transmite a lo largo de la línea de actuación3.
Históricamente, 14,5° era un estándar común. Sin embargo, producía dientes propensos a la socavación. Esto debilita la base del diente.
Para solucionarlo, la industria ha optado en gran medida por un ángulo de presión de 20°. En PTSMAKE, solemos recomendar 20° para la mayoría de las aplicaciones. Proporciona una base dentada más ancha y fuerte, mejorando la capacidad de carga.
También existe un estándar de 25°. Ofrece una resistencia dental aún mayor. Sin embargo, tiene sus inconvenientes. Aumenta la fuerza radial sobre los rodamientos, lo que puede provocar un mayor desgaste y más ruido de funcionamiento.
Elegir el ángulo correcto requiere un cuidadoso análisis de ingeniería. Ayudamos a los clientes a sopesar estos factores para optimizar sus diseños. No es solo un número, define cómo se comporta el sistema.
Comparación de ángulos de presión comunes
| Ángulo | Pros | Contras |
|---|---|---|
| 14.5° | Funcionamiento más suave y silencioso; menor carga sobre los cojinetes. | Diente más débil; propenso al socavado. |
| 20° | Buen equilibrio entre resistencia y eficacia; estándar del sector. | Elección estándar, pocos contras específicos. |
| 25° | Perfil del diente más resistente; gran capacidad de carga. | Mayores cargas sobre los rodamientos; pueden ser más ruidosas. |
El ángulo de presión dicta la transmisión de fuerzas entre los dientes del engranaje. La norma común de 20° equilibra la resistencia del diente con la carga del rodamiento y la tensión de contacto. Los ángulos más altos aumentan la resistencia, pero también la tensión y el ruido potencial, lo que crea un equilibrio crítico en el diseño.
Addendum y Dedendum como dimensiones radiales
El addendum y el dedendum son dimensiones radiales clave. Se miden a partir del círculo primitivo. Una va hacia arriba y la otra hacia abajo.
Juntos, definen la altura total de un diente de engranaje. Esto es crucial para que los engranajes encajen y funcionen juntos.
El diente sobre el círculo polar
La adición es la altura desde el círculo primitivo hasta la parte superior del diente. Determina hasta dónde se extiende un diente.
El diente bajo el círculo polar
El dedendum es la profundidad desde el círculo primitivo hasta la raíz del diente. Define el espacio para la punta del diente de la rueda dentada de contacto.
| Dimensión | Ubicación | Función |
|---|---|---|
| Anexo | Por encima de Pitch Circle | Define la altura de la punta del diente |
| Dedendum | Por debajo de Pitch Circle | Define la profundidad de la raíz del diente |
Estas medidas no son aleatorias. Controlan directamente la profundidad de trabajo de la malla del engranaje.

Entender cómo funcionan estas dimensiones es fundamental. Ellas dictan si los engranajes engranan suavemente o fallan prematuramente. Estas dimensiones radiales son parámetros críticos de los engranajes (Parámetros de los engranajes).
El addendum de una rueda dentada debe engranar correctamente con el dedendum de su compañera. Este espacio de interacción se denomina profundidad de trabajo. Es la profundidad de engrane entre dos engranajes.
Se deja un pequeño espacio, conocido como espacio libre, en la parte inferior del espacio dental. De este modo se evita que la parte superior de un diente choque con la parte inferior del espacio interdental correspondiente. Una holgura adecuada es esencial.
En proyectos anteriores de PTSMAKE, hemos visto diseños en los que estos valores estaban desviados por pequeñas cantidades. Este error aparentemente pequeño puede causar problemas importantes. Entre ellos, ruido excesivo, vibraciones y desgaste acelerado. Incluso puede provocar un fallo completo del sistema.
Unas dimensiones inadecuadas pueden provocar interferencias4donde los dientes chocan físicamente en lugar de rodar suavemente.
Por eso la precisión no es negociable en la fabricación de engranajes.
Escenarios de compromiso
| Escenario | Relación Adenda/Dedendum | Resultado |
|---|---|---|
| Correcto | Calculado correctamente | Transmisión de potencia suave y eficaz |
| Demasiado grande | Profundidad de trabajo excesiva | Tensión alta |
| Demasiado pequeño | Compromiso insuficiente | Deslizamiento, holgura, bajo contacto |
En PTSMAKE, utilizamos mecanizado CNC avanzado para mantener tolerancias extremadamente ajustadas en estas características. Nos aseguramos de que cada engranaje que producimos cumpla las especificaciones exactas de diseño para un rendimiento fiable. Esta precisión evita problemas de acoplamiento.
Addendum y dedendum son medidas radiales a partir del círculo primitivo. Definen la altura del diente y la profundidad de la raíz. Estas dimensiones son fundamentales para determinar la profundidad de trabajo y garantizar un engranaje suave y fiable, evitando fallos operativos.
¿Para qué sirve la holgura en un sistema de engranajes?
El juego es la separación entre los dientes de dos engranajes. A menudo se considera un defecto, pero es una característica esencial del diseño.
Esta separación garantiza que los engranajes no se atasquen. Proporciona espacio para que la lubricación forme una película protectora entre los dientes. Esto evita el contacto directo entre metales.
Por qué es necesaria la autorización
Sin holgura, pueden surgir varios problemas. La dilatación térmica es uno de los principales. Al funcionar, los engranajes se calientan y se dilatan. La holgura les da espacio para crecer.
Las tolerancias de fabricación también influyen. Comprender todos los factores, incluidos datos clave como los parámetros de los engranajes, es vital para un diseño adecuado.
| Factor | Motivo del contragolpe |
|---|---|
| Expansión térmica | Permite que los engranajes se expandan con el calor sin atascarse. |
| Tolerancia de fabricación | Tiene en cuenta las pequeñas variaciones en las dimensiones de los engranajes. |
| Lubricación | Garantiza la formación de una película fluida entre los dientes. |

El compromiso: precisión frente a rendimiento
El principal reto del contragolpe es encontrar el equilibrio adecuado. Implica una compensación directa con la precisión posicional. Más holgura significa menos precisión. Esto puede ser un problema en robótica o máquinas CNC.
En estas aplicaciones, cualquier "inclinación" en el tren de engranajes reduce la precisión. El sistema podría no responder instantáneamente a los cambios de dirección.
Encontrar el punto óptimo
Sin embargo, la holgura cero no siempre es el objetivo. Un juego insuficiente puede ser tan malo como un juego excesivo. Una holgura insuficiente puede provocar un desgaste prematuro y grandes esfuerzos. También aumenta la fricción y la generación de calor.
Esto puede causar lo que se conoce como Interferencias de malla5en el que los dientes se atascan en lugar de rodar suavemente. En proyectos anteriores de PTSMAKE, hemos descubierto que el juego ideal depende totalmente de los requisitos específicos de la aplicación.
| Nivel de holgura | Precisión posicional | Riesgo de interferencia |
|---|---|---|
| Alta | Bajo | Bajo |
| Óptimo | Alta | Bajo |
| Bajo / Cero | Muy alta | Alta |
Trabajamos en estrecha colaboración con los clientes para definir estas necesidades. Nos aseguramos de que los engranajes fabricados tengan el juego óptimo tanto para la longevidad como para la precisión.
La holgura es una separación intencionada entre los dientes de un engranaje. Es crucial para evitar atascos causados por el calor y las variaciones de fabricación. La clave está en equilibrar esta holgura necesaria con el nivel requerido de precisión posicional para la aplicación específica.
¿Qué es el diámetro del círculo primitivo (d) y por qué es crucial?
El círculo de paso es un círculo imaginario en un engranaje. Es la línea teórica donde dos engranajes ruedan juntos sin ningún deslizamiento. Imagínatelo como dos cilindros perfectos rodando uno contra otro.
Este concepto es la base del diseño de engranajes. Es la referencia principal para casi todas las demás dimensiones de engranajes. Sin él, los cálculos serían increíblemente complejos. Todos los parámetros esenciales de los engranajes se derivan de esta única característica.
| Parámetro derivado de PCD | Función |
|---|---|
| Módulo | Define el tamaño del diente |
| Distancia al centro | Establece la separación entre marchas |
| Apéndice/Dedendum | Determina la altura del diente |
| Grosor del diente | Afecta a la fuerza y al contragolpe |

El corazón teórico del engranaje
El círculo de paso no es una parte física del engranaje. No se puede tocar. Es un concepto puramente teórico que simplifica las complejas interacciones entre los dientes del engranaje en un movimiento de rodadura puro. Esta idealización es vital para el diseño inicial y el cálculo.
En los proyectos de PTSMAKE, siempre empezamos por aquí. Este círculo imaginario dicta la relación de velocidad del engranaje y su ubicación exacta en relación con su engranaje acoplado. Es el punto de partida de un buen diseño.
Del concepto ideal a la realidad física
Mientras que en el círculo primitivo nos imaginamos una rodadura pura, los dientes de los engranajes reales experimentan tanto la rodadura como el deslizamiento. Esta combinación es necesaria para una transferencia de potencia suave. La forma específica del diente del engranaje, a menudo un perfil de evolvente6está diseñado para gestionar este movimiento. Garantiza una velocidad angular constante, incluso con el deslizamiento. Entender qué parámetros del engranaje son críticos es el primer paso.
La clave de la distancia al centro
El diámetro del círculo primitivo determina directamente la distancia central entre dos engranajes. La fórmula es sencilla pero eficaz:
Distancia entre ejes (C) = (PCD de la marcha 1 + PCD de la marcha 2) / 2
Este cálculo es fundamental. Una distancia entre ejes incorrecta conduce a un mallado inadecuado, causando ruido excesivo, desgaste y posibles fallos.
| Engranaje 1 PCD (mm) | Engranaje 2 PCD (mm) | Distancia entre ejes requerida (mm) |
|---|---|---|
| 50 | 100 | 75 |
| 60 | 60 | 60 |
| 40 | 80 | 60 |
El círculo primitivo es una línea de referencia imaginaria pero fundamental en el diseño de engranajes. Simplifica las complejas interacciones de los dientes en un movimiento de rodadura puro, sirviendo de base para calcular todas las demás dimensiones críticas y la distancia crucial entre centros de engranajes.
¿Cuál es la distancia entre ejes (a) en un par de engranajes?
La distancia entre ejes, denominada "a", es un parámetro fundamental. Es simplemente la distancia entre los centros de dos engranajes acoplados.
Esta dimensión no es sólo un número. Dicta toda la disposición física de una caja de cambios. Determina cómo y dónde se asientan los engranajes.
Acertar con esta distancia es fundamental. Garantiza una transmisión fluida de la potencia. Una separación incorrecta provoca problemas de funcionamiento.
| Componente | Descripción |
|---|---|
| Engranaje 1 Centro | El eje de rotación de la primera rueda dentada. |
| Engranaje 2 Centro | El eje de rotación del segundo engranaje. |
| Distancia al centro (a) | La distancia en línea directa entre estos dos centros. |
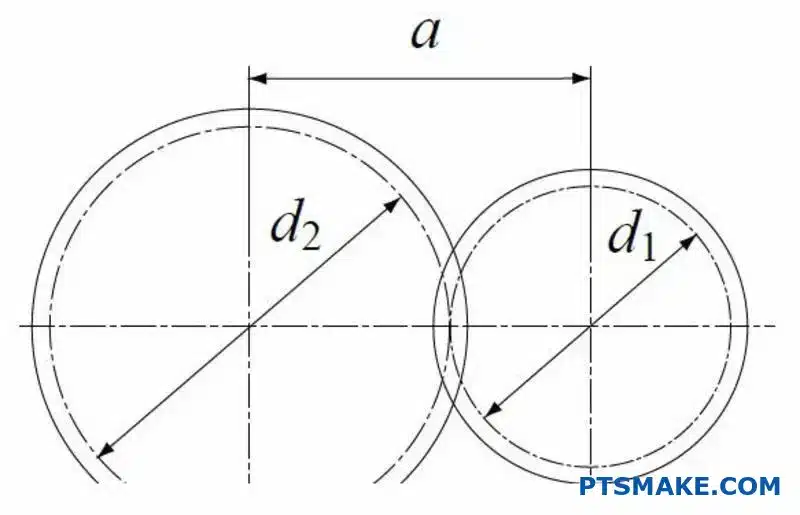
Calcular la distancia entre ejes es sencillo. Es la mitad de la suma de las dos marchas. diámetros de paso7. Esta relación directa es crucial para el diseño.
La fórmula estándar es sencilla:
a = (d1 + d2) / 2
Toma, d1 y d2 representan los diámetros de los dos engranajes. Este cálculo es un punto de partida para el diseño de cualquier caja de cambios.
También podemos expresarlo mediante el módulo (m) y el número de dientes (z).
a = m * (z1 + z2) / 2
Esto muestra cómo se relacionan los parámetros clave del engranaje. Cuando los clientes preguntan "Parámetros del engranaje" (¿cuáles son los parámetros de un engranaje?), solemos empezar por aquí. Explicamos cómo están conectados el módulo, los dientes y la distancia entre ejes.
En los proyectos que gestionamos en PTSMAKE, la distancia entre ejes es una dimensión crítica. Cuando mecanizamos por CNC la carcasa de una caja de cambios, este valor determina la ubicación exacta de los orificios de los rodamientos.
Cualquier desviación causa problemas. Una distancia demasiado grande crea un exceso de holgura y ruido. Una distancia demasiado pequeña provoca atascos y un rápido desgaste. La precisión del alojamiento influye directamente en el rendimiento del engranaje.
| Factor | Consecuencia de una distancia entre ejes incorrecta |
|---|---|
| Demasiado grande | Mayor holgura, ruido, posible salto de dientes. |
| Demasiado pequeño | Atasco del engranaje, desgaste excesivo, alta fricción. |
La disposición física de todo el sistema depende de este valor. Influye en el tamaño de la carcasa, la colocación de los rodamientos y el proceso de montaje final.
La distancia entre ejes es el espacio entre dos ejes de engranaje. Se calcula a partir de los diámetros de paso. Esta medida es la base del diseño de la caja de cambios y garantiza que los engranajes engranen correcta y eficazmente.
¿Qué define la anchura de la cara (b) de un engranaje?
La anchura de la cara, denominada "b", es un parámetro crítico del engranaje. Parece sencillo, pero tiene una enorme repercusión. Es la longitud del diente paralela al eje del engranaje.
Piense que es el grosor del engranaje de delante hacia atrás. Una cara más ancha significa más material.
Por qué es importante la anchura de la cara
Esta dimensión está directamente relacionada con la resistencia. Determina el par que puede soportar una rueda dentada. También afecta a la distribución de la carga en la superficie del diente. Comprender estos parámetros es fundamental.
| Característica | Ancho de cara estrecho | Ancho de cara ancho |
|---|---|---|
| Capacidad de par | Baja | Más alto |
| Distribución de la carga | Más concentrados | Más repartidos |
| Coste del material | Baja | Más alto |
Una marcha más ancha suele ser más fuerte. Pero no siempre es mejor. La anchura óptima depende de la aplicación específica.

Capacidad de par y distribución de la carga
La función principal de un engranaje es transmitir par. La anchura de la cara es fundamental para esta tarea. Una cara más ancha proporciona una mayor superficie de contacto para el engrane de los dientes. Esto permite al engranaje soportar mayores cargas sin fallar. Es una relación directa.
Esta mayor superficie también mejora la distribución de la carga. En lugar de concentrar la fuerza en un pequeño punto, la carga se reparte por toda la longitud del diente. Esto reduce significativamente la tensión sobre el material. Una cara más ancha reduce eficazmente la Tensión de contacto hertziana8 en la superficie del diente.
Los inconvenientes de una cara más ancha
Sin embargo, una mayor anchura de cara no es una solución universal. Plantea problemas. El más importante es la sensibilidad a la alineación. Si los engranajes anchos no están perfectamente alineados, la carga se concentrará en un borde. Esto provoca un desgaste desigual y puede conducir a un fallo prematuro.
En PTSMAKE, nuestro mecanizado CNC garantiza una alineación perfecta. Ayudamos a los clientes a encontrar el equilibrio adecuado. Se trata de maximizar la resistencia sin comprometer la fiabilidad debido a las limitaciones de fabricación.
| Factor de diseño | Impacto del aumento de la anchura de la cara |
|---|---|
| Transmisión de par | Aumenta la capacidad |
| Resistencia a la flexión | Aumenta |
| Sensibilidad de alineación | Aumenta el riesgo de carga en los bordes |
| Coste de fabricación | Aumentos debidos a más material |
La anchura de la cara (b) es la longitud del diente del engranaje. Está directamente relacionada con la capacidad de par y la distribución de carga de un engranaje. Una cara más ancha aumenta la resistencia, pero exige una alineación más precisa, una consideración clave en aplicaciones de alto rendimiento.
¿Qué es el cambio de perfil (o modificación de adenda)?
El desplazamiento de perfil es una técnica clave en el diseño de engranajes. Consiste en desplazar intencionadamente la herramienta de corte. Este desplazamiento es relativo al centro de la pieza bruta del engranaje.
Este ajuste no es aleatorio. Es una modificación calculada. Llamamos a la cantidad de desplazamiento "coeficiente de desplazamiento del perfil (x)".
Su principal objetivo es resolver problemas de diseño específicos. Lo utilizamos para evitar el destalonado en engranajes pequeños. También ayuda a ajustar la distancia central entre dos engranajes.
Los clientes preguntan a menudo: "¿Parámetros de un engranaje?". (¿Cuáles son los parámetros de una marcha?). El cambio de perfil es uno crucial que repercute directamente en el rendimiento.
| Propósito | Descripción |
|---|---|
| Evitar la subcotización | Evita el debilitamiento de la base dentada en engranajes con pocos dientes. |
| Ajustar distancia central | Permite distancias entre ejes no estándar sin cambiar el tamaño del engranaje. |

Este desplazamiento deliberado de la herramienta de corte es lo que define el desplazamiento del perfil. Un coeficiente positivo (x > 0) significa que alejamos la herramienta del centro del engranaje. El resultado es una raíz de diente más gruesa y fuerte. Es el principal método para evitar el destalonado en piñones con un bajo número de dientes.
Por el contrario, un coeficiente negativo (x < 0) acerca la herramienta al centro. Esto crea un diente más fino. Normalmente utilizamos un desplazamiento negativo en la rueda más grande de un par. Esto se hace para conseguir una distancia entre ejes específica, a menudo reducida.
Según mi experiencia en PTSMAKE, equilibrar estos cambios es crucial. Un desplazamiento positivo puede fortalecer el diente. Pero demasiado puede provocar puntas de diente puntiagudas y un aumento de la fricción por deslizamiento. Afecta a la perfil de evolvente9.
La elección del coeficiente es un cálculo preciso. Influye directamente en la resistencia del engranaje, su vida útil y el ruido de funcionamiento. Es un compromiso que gestionamos cuidadosamente en cada proyecto.
| Tipo de turno | Posición de la herramienta | Efecto primario |
|---|---|---|
| Positivo (+x) | Alejado del centro | Raíz del diente más fuerte, evita el socavado |
| Cero (x=0) | Posición estándar | Perfil estándar del diente del engranaje |
| Negativo (-x) | Se movió hacia el centro | Diente más fino, reduce la distancia entre ejes |
El desplazamiento de perfil es un desplazamiento estratégico de la herramienta de tallado de engranajes. Tiene dos objetivos principales. Evita la socavación del diente en piñones pequeños para una mayor resistencia. También permite ajustar con flexibilidad la distancia entre ejes del engranaje.
¿Qué es el radio del filete raíz (ρf) y cuál es su significado?
El filete de raíz es la transición curva en la base de un diente de engranaje. Es una característica de diseño crítica. Su función principal es reducir la concentración de tensiones en la raíz del diente.
El papel del filete radicular
Piense en ello como una curva suave en lugar de una curva cerrada. Esta curva distribuye las fuerzas de forma más uniforme. Esto evita que se formen grietas. Cuando los clientes preguntan por los parámetros clave del engranaje (Parámetros del engranaje), el fileteado de la raíz es siempre una de las principales consideraciones para la durabilidad.
| Característica | Nivel de estrés | Fatiga Vida |
|---|---|---|
| Esquina afilada | Alta | Bajo |
| Filete redondeado | Bajo | Alta |
Un fileteado correctamente diseñado es crucial para evitar el fallo por fatiga de flexión de los dientes. Prolonga considerablemente la vida útil del engranaje.
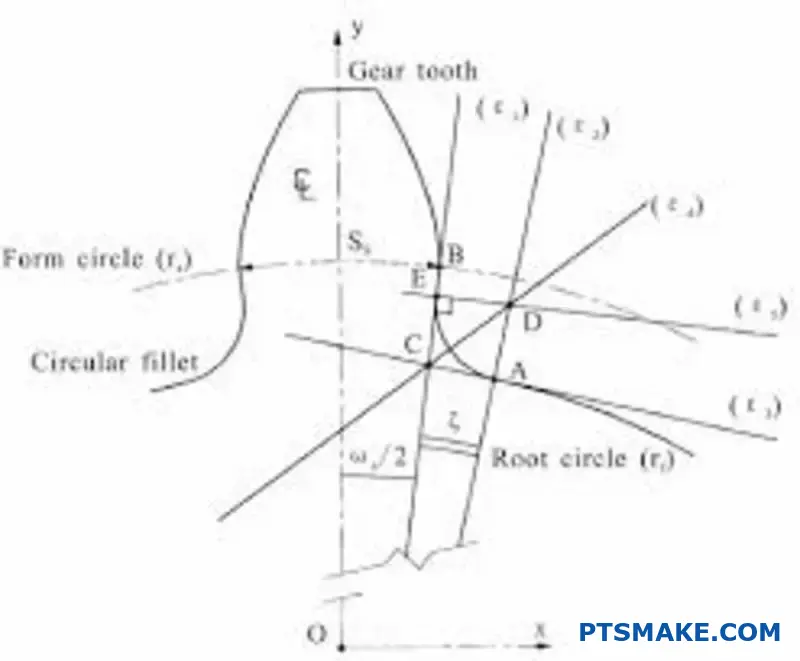
Prevención de la fatiga por flexión
La raíz del diente es la zona más vulnerable. Experimenta la mayor tensión de flexión durante el funcionamiento. Sin un filete, esta tensión se concentra en la esquina afilada. Esta es una de las principales causas de fallo por fatiga.
Un radio de filete más grande suele significar una tensión menor. Sin embargo, hay un límite. Si el radio es demasiado grande, puede interferir con el diente del engranaje de contacto. Esto provoca un problema denominado interferencia trocoidal. Encontrar el radio óptimo es un acto de equilibrio.
En nuestro trabajo en PTSMAKE, utilizamos a menudo el análisis por elementos finitos (FEA). Esto nos ayuda a simular y encontrar el radio de filete perfecto. Maximiza la resistencia sin causar interferencias. Este cuidadoso análisis reduce el concentración de tensiones10 de raíz.
Radio del filete frente a tensión
La relación es clara. Un filete más grande y liso es mejor para la durabilidad. Según nuestras pruebas, el impacto es significativo.
| Radio del filete (ρf) | Concentración relativa de estrés |
|---|---|
| Pequeño (afilado) | 2.5x |
| Medio | 1.8x |
| Óptimo (Grande) | 1.2x |
Esto demuestra por qué es tan importante controlar con precisión el radio del filete de la raíz durante el mecanizado CNC. Influye directamente en la fiabilidad y el rendimiento del engranaje.
El filete radicular no es sólo una pequeña curva. Es un elemento de diseño crítico que reduce la concentración de tensiones en la base del diente. Esto evita directamente los fallos por fatiga y garantiza la fiabilidad a largo plazo del sistema de engranajes.
¿En qué se diferencian fundamentalmente los parámetros de los engranajes rectos, helicoidales y cónicos?
Aunque todos los engranajes comparten parámetros básicos como el módulo y el diámetro de paso, las diferencias fundamentales surgen de su geometría. Cada tipo añade parámetros únicos para adaptarse a su función específica.
Las ruedas dentadas rectas son las más sencillas. Los engranajes helicoidales y cónicos introducen dimensiones angulares cruciales. Estos añadidos no son opcionales, sino que definen el funcionamiento de los engranajes.
Comprender cuáles son los parámetros de los engranajes (Gear Parameters) de cada tipo es clave. Dicta su aplicación y rendimiento.
| Tipo de engranaje | Clave Parámetro único | Propósito |
|---|---|---|
| Engranaje recto | Ninguno (dientes rectos) | Transmisión de potencia por ejes paralelos |
| Engranaje helicoidal | Ángulo de la hélice (β) | Funcionamiento más suave y silencioso |
| Engranaje cónico | Ángulos del cono (Pitch, Root) | Eje acodado Transmisión de potencia |

Veamos por qué son necesarios estos parámetros específicos. Los engranajes rectos tienen dientes rectos paralelos al eje del engranaje. Su conjunto de parámetros es la base para todos los tipos de engranajes. Es sencillo y eficaz para ejes paralelos.
Los engranajes helicoidales introducen el ángulo de hélice (β). Este ángulo es la razón de su funcionamiento más suave y silencioso. Los dientes acodados engranan gradualmente en toda su cara, no todos a la vez. Esto reduce los golpes y el ruido. Este ángulo también introduce un empuje axial11 componente, que es una consideración clave en la selección de rodamientos.
Los engranajes cónicos están diseñados para ejes que se cruzan, normalmente a 90 grados. Sus ángulos cónicos son esenciales. Estos ángulos definen la forma cónica de la pieza bruta del engranaje. Sin el ángulo correcto del cono de paso, los dientes no engranarían correctamente. Se atascarían o tendrían un juego excesivo. En PTSMAKE, siempre hacemos hincapié en que estos ángulos deben calcularse con precisión para que el sistema funcione correctamente.
| Parámetro | Por qué es necesario | Impacto en el diseño |
|---|---|---|
| Ángulo de la hélice (β) | Permite el engrane gradual de los dientes. | Crea una transferencia de potencia más suave, pero también carga axial. |
| Ángulos del cono | Permite el engrane de engranajes en ejes de intersección. | Define la forma fundamental para la transmisión en ángulo. |
En resumen, los engranajes rectos se basan en parámetros básicos. Los engranajes helicoidales añaden el ángulo de hélice para mayor suavidad, mientras que los engranajes cónicos utilizan ángulos de cono para transmitir potencia entre ejes que se cruzan. Estos parámetros únicos vienen dictados por su geometría central y la aplicación prevista.
¿Cuál es la relación entre módulo, número de dientes y diámetro?
En el diseño de engranajes, el módulo, el número de dientes y el diámetro no son elecciones separadas. Forman un equipo. Un cambio en uno de ellos repercute directamente en los demás. Esta relación se rige por una fórmula fundamental.
Comprender este principio básico es esencial. Evita errores costosos y garantiza un engranaje perfecto. Es la base de todos los cálculos de engranajes.
Exploremos esta sencilla pero poderosa conexión.

La relación se reduce a una fórmula sencilla. Es la clave para descifrar el diseño de los engranajes y una parte esencial de la comprensión de los Parámetros de Engranaje (cuáles son los parámetros de un engranaje).
La fórmula básica
La ecuación fundamental es:
Diámetro de paso (d) = Módulo (m) × Número de dientes (Z)
Esta fórmula muestra una relación directa. Si conoces dos valores cualesquiera, siempre puedes encontrar el tercero. Es así de sencillo. Este cálculo nos da el Paso Diámetro12una medida vital para la funcionalidad del engranaje.
Cómo se influyen mutuamente
Veámoslo en acción. Imaginemos que tenemos un módulo fijo de 2. Al cambiar el número de dientes cambia directamente el diámetro.
| Módulo (m) | Número de dientes (Z) | Diámetro de paso (d) |
|---|---|---|
| 2 | 20 | 40 mm |
| 2 | 40 | 80 mm |
| 2 | 60 | 120 mm |
Como puede ver, al duplicar los dientes se duplica el diámetro.
Ahora bien, ¿y si necesitamos un diámetro concreto, digamos 100 mm? Podemos conseguirlo con distintas combinaciones de módulo y dientes.
| Diámetro del objetivo (d) | Módulo (m) | Número de dientes (Z) |
|---|---|---|
| 100 mm | 2 | 50 |
| 100 mm | 4 | 25 |
| 100 mm | 5 | 20 |
En PTSMAKE, utilizamos este principio a diario para diseñar soluciones que se ajusten a los requisitos precisos de espacio y resistencia de nuestros clientes.
La relación es clara: el módulo, el número de dientes y el diámetro de paso están intrínsecamente relacionados. No se puede modificar uno de estos parámetros básicos sin afectar al menos a uno de los otros. Se trata de una regla innegociable en el diseño mecánico.
¿Cómo afecta el ángulo de presión a la resistencia del diente y a la relación de contacto?
Elegir el ángulo de presión adecuado es un acto de equilibrio crítico en el diseño de engranajes. Es una decisión fundamental que cambia directamente la resistencia del diente por un funcionamiento suave.
Entender el compromiso
Un ángulo de presión mayor, como 25°, crea una base dentada más ancha y robusta. Esto aumenta la resistencia y la capacidad de carga.
Por el contrario, un ángulo menor, como 14,5°, da como resultado una mayor relación de contacto. Esto significa que se engranan más dientes a la vez, lo que se traduce en una transmisión de potencia más suave y silenciosa. Su elección depende totalmente de las exigencias de la aplicación. En este sentido, es fundamental tener en cuenta cuestiones como los parámetros de los engranajes.
| Ángulo de presión | Ventaja principal | Desventaja principal |
|---|---|---|
| Mayor (por ejemplo, 25°) | Mayor resistencia dental | Menor relación de contacto (más ruidoso) |
| Más pequeño (por ejemplo, 14,5°) | Mayor relación de contacto (más suave) | Resistencia dental inferior |
Este compromiso básico influye en muchos aspectos del rendimiento del engranaje.

Ángulos mayores vs. menores: Una mirada más profunda
En nuestros proyectos en PTSMAKE, el ángulo de presión es uno de los primeros parámetros que confirmamos con los clientes. Las implicaciones son importantes para la fabricación y el rendimiento final.
La fuerza de un ángulo de 25
Un mayor ángulo de presión crea un diente con una base gruesa y resistente. Esta geometría es excelente para aplicaciones que implican un par elevado y cargas pesadas. Reduce significativamente la tensión en la raíz del diente.
Este diseño también es menos susceptible a subcotización13 durante la fabricación. Aquí es donde la herramienta de corte elimina material de la base del diente del engranaje, debilitándolo.
La suavidad de un ángulo de 14,5
Aunque no es tan fuerte, un ángulo de presión menor ofrece una suavidad superior. Con una mayor relación de contacto, la carga se distribuye sobre más dientes simultáneamente.
Esto se traduce en menos vibraciones y un funcionamiento más silencioso. Suele ser la opción preferida para instrumentos de precisión y aplicaciones en las que el bajo nivel de ruido es un requisito fundamental. Sin embargo, los dientes son más finos y más propensos a doblarse bajo tensión.
| Característica | Mayor ángulo de presión (25°) | Ángulo de presión menor (14,5°) |
|---|---|---|
| Base del diente | Amplio y fuerte | Estrecho y débil |
| Operación | Puede ser más ruidoso | Silencioso y suave |
| El mejor caso de uso | Maquinaria industrial de alta carga | Instrumentos de precisión, sistemas de bajo ruido |
La elección del ángulo de presión es un compromiso de diseño crucial. Hay que equilibrar la necesidad de resistencia de los dientes y gran capacidad de carga con el requisito de un funcionamiento suave y silencioso. La decisión final depende siempre de las necesidades específicas de su aplicación.
¿Cuál es el concepto de "marcha estándar" frente a "marcha modificada"?
Los engranajes pueden clasificarse en dos tipos principales. Se trata de los engranajes estándar y los engranajes modificados. Esta distinción es crucial en el diseño y la fabricación.
Los engranajes estándar se ajustan a parámetros reconocidos internacionalmente. Esto incluye un ángulo de presión estándar y un desplazamiento de perfil cero. Son la base para el diseño de engranajes.
Sin embargo, las marchas modificadas se apartan de estas normas. Hacemos estos cambios por razones específicas. Esto garantiza que el sistema de engranajes funcione perfectamente en su aplicación exclusiva.
Principales diferencias
| Característica | Engranaje estándar | Engranaje modificado |
|---|---|---|
| Bases del diseño | Sigue las normas establecidas | Desviaciones por necesidades específicas |
| Cambio de perfil | Cero | Positivo o negativo |
| Distancia al centro | Estándar | Puede ser no estándar |
| Aplicación | De uso general | Optimizado para el rendimiento |

Por qué modificamos los engranajes
Quizá se pregunte por qué íbamos a cambiar un diseño estándar en perfecto estado. La realidad es que las aplicaciones del mundo real suelen presentar retos únicos. Los engranajes estándar son un buen punto de partida, pero no siempre son la solución definitiva.
Distancias entre centros no estándar
Una de las razones más comunes para la modificación es una distancia entre ejes no estándar. Las carcasas de las máquinas o los componentes existentes suelen dictar la distancia entre dos ejes de engranaje.
Si esta distancia no coincide con un par de engranajes estándar, debemos ajustarla. Utilizamos un cambio de perfil14 para que los engranajes engranen correctamente sin holguras ni atascos. Se trata de un ajuste frecuente en nuestro trabajo en PTSMAKE.
Optimizar el rendimiento
La modificación es también una poderosa herramienta para ajustar el rendimiento. Ajustando parámetros específicos, podemos mejorar las características de un engranaje. Cuando los clientes preguntan por los parámetros de un engranaje que pueden ajustarse, solemos hablar de estas modificaciones.
Estos son algunos de los objetivos de optimización más comunes:
| Objetivo de optimización | Método de modificación | Beneficio |
|---|---|---|
| Aumentar la fuerza | Cambio de perfil positivo | Previene la socavación, engrosa la raíz del diente |
| Reducir el ruido | Ajustar la relación de contacto | Garantiza un funcionamiento más suave y silencioso |
| Mejorar la vida útil | Deslizamiento específico de la balanza | Distribuye la carga de forma más uniforme |
| Evitar interferencias | Ajustes del relieve de la punta | Evita la colisión de la punta del diente |
Estos cambios a medida transforman un componente estándar en una pieza de alto rendimiento, perfectamente adaptada a su tarea específica.
En resumen, las marchas estándar se basan en especificaciones universales. Los engranajes modificados son soluciones a medida. Responden a limitaciones prácticas, como espaciamientos no estándar o la necesidad de una mayor resistencia, un funcionamiento más silencioso y una vida útil más larga en aplicaciones específicas.
¿Cómo influyen los parámetros de los engranajes cilíndricos (ángulo de hélice) en el empuje axial?
El ángulo de hélice de un engranaje es un clásico de la ingeniería. Es la característica que confiere a los engranajes helicoidales su funcionamiento suave y silencioso.
Sin embargo, este acoplamiento en ángulo crea un efecto secundario. Genera una fuerza de empuje axial a lo largo del eje del engranaje. Esta fuerza debe gestionarse correctamente.
Sin un apoyo adecuado, este empuje puede causar problemas importantes en su montaje. Es un factor crítico a tener en cuenta en el diseño.
| Parámetro | Efecto positivo | Efecto negativo |
|---|---|---|
| Ángulo de la hélice | Funcionamiento más suave y silencioso | Genera empuje axial |
Esta relación causa-efecto es fundamental en el diseño de los engranajes cilíndricos. Hay que tener en cuenta los dos lados de la ecuación.

El origen del empuje axial
Cuando los dientes de los engranajes helicoidales engranan, la fuerza no se aplica perpendicularmente al eje del árbol como en los engranajes rectos. El ángulo de los dientes divide la fuerza resultante15 en dos componentes principales.
Una es la fuerza tangencial, que transmite el par. La otra es la fuerza axial, o empuje, que empuja el engranaje lateralmente a lo largo de su eje. Un mayor ángulo de hélice significa un mayor componente de empuje axial.
Gestión del empuje axial con rodamientos
Esta carga axial debe soportarse para evitar la desalineación y el fallo del engranaje. Aquí es donde los rodamientos se vuelven críticos.
No puede limitarse a utilizar rodamientos radiales estándar. Necesita rodamientos diseñados para soportar cargas axiales, tales como:
- Rodamientos de rodillos cónicos
- Rodamientos de bolas de contacto angular
- Rodamientos axiales específicos
En nuestros proyectos en PTSMAKE, la selección del sistema de rodamientos adecuado es una parte clave de la consulta de diseño. Añade complejidad y coste, pero no es negociable para la fiabilidad.
La solución del engranaje en espiga
Existe un ingenioso diseño que elimina este problema: el engranaje de espiga. Se trata de dos engranajes helicoidales, uno a derechas y otro a izquierdas, unidos entre sí.
Los ángulos de hélice opuestos generan fuerzas axiales de empuje iguales y opuestas. Estas fuerzas se anulan mutuamente en el interior del engranaje.
| Característica | Engranaje helicoidal | Engranaje en espiga |
|---|---|---|
| Empuje axial | Presente | Autocancelación |
| Necesidades de rodamientos | Rodamientos de empuje necesarios | Rodamientos Simpler OK |
| Fabricación | Más sencillo | Más complejo y costoso |
Esta elegante solución simplifica los requisitos de los rodamientos, pero dificulta la fabricación del propio engranaje.
La ventaja del ángulo de hélice para un funcionamiento suave se consigue a costa de crear un empuje axial. Esta fuerza requiere la gestión de rodamientos específicos, lo que añade complejidad. Los engranajes en espina de pescado ofrecen una solución integrada al anular este empuje internamente.
¿Qué es la relación de contacto y qué parámetros influyen en ella?
La relación de contacto es un parámetro crítico del engranaje. Indica el número medio de dientes en contacto en cada momento. Piense en ello como una medida del solapamiento del engranaje.
Para que la transmisión de potencia sea fluida y continua, este número debe ser siempre mayor que uno. Varias opciones de diseño influyen en esta relación crucial. Entender cuáles son estos parámetros de un engranaje es clave.
Factores clave que influyen en la proporción de contactos
A continuación se indican los principales factores que tenemos en cuenta en nuestros diseños en PTSMAKE. Cada uno de ellos puede ajustarse para lograr el rendimiento deseado por nuestros clientes.
| Parámetro | Efecto general sobre la relación de contacto |
|---|---|
| Ángulo de presión | Un ángulo menor suele aumentarlo. |
| Anexo | Una adenda más grande la aumenta. |
| Cambio de perfil | Un cambio positivo suele aumentarla. |

Una mayor relación de contacto es casi siempre mejor. Nosotros buscamos un valor superior a 1,2 en la mayoría de las aplicaciones. ¿Por qué? Porque garantiza que un nuevo par de dientes se engrane antes de que se desenganche el par anterior.
Este solapamiento es el secreto del funcionamiento suave y silencioso de los engranajes. Elimina los momentos de contacto de un solo diente, que pueden causar fluctuaciones de par, vibraciones y ruido. Distribuye la carga entre más dientes.
El papel del ángulo de presión
Un ángulo de presión menor, como 14,5°, crea una línea de contacto más larga en comparación con un ángulo de 20°. Esta trayectoria más larga aumenta directamente la relación de contacto, favoreciendo un engrane más suave. Sin embargo, puede resultar en una base de diente más débil.
Apéndice y cambio de perfil
Al aumentar el addendum (la altura del diente por encima del círculo primitivo) se alarga la punta del diente. Esto alarga físicamente el longitud de la trayectoria de contacto16. Un desplazamiento positivo del perfil consigue un efecto similar, desplazando el perfil del diente hacia fuera.
En proyectos anteriores de PTSMAKE, hemos equilibrado cuidadosamente estos parámetros. Optimizamos para conseguir una elevada relación de contacto manteniendo la resistencia del diente y evitando interferencias.
| Ratio de contacto | Característica de rendimiento |
|---|---|
| < 1.0 | Inaceptable; contacto intermitente |
| 1.0 - 1.2 | Aceptable, pero puede tener algo de ruido |
| > 1.2 | Deseable; funcionamiento suave y silencioso |
| > 2.0 | Alto rendimiento; muy suave (helicoidal) |
La relación de contacto es un parámetro clave del rendimiento de los engranajes. Define la suavidad de funcionamiento. Está directamente influida por parámetros de diseño como el ángulo de presión, la adición y el desplazamiento del perfil. Una relación superior a 1,2 es ideal para minimizar el ruido y las vibraciones.
¿En qué se diferencian los parámetros de los engranajes helicoidales (avance, ángulo de avance)?
Cuando los clientes preguntan "¿cuáles son los parámetros de los engranajes?", suelen pensar en engranajes rectos o helicoidales. Pero los engranajes helicoidales tienen un lenguaje único. Sus parámetros clave son el avance y el ángulo de avance, no el paso.
Estas dos características lo definen todo. Determinan la elevada relación de reducción del engranaje y su movimiento específico. Comprenderlas es crucial para un diseño adecuado.
Parámetros del engranaje recto frente al engranaje helicoidal
He aquí una rápida comparación:
| Tipo de parámetro | Engranaje recto/hélice | Engranaje helicoidal |
|---|---|---|
| Métrica primaria | Paso (Diametral/Módulo) | Plomo |
| Ángulo métrico | Ángulo de presión | Ángulo de ataque |
| Ratio Conductor | Proporción de dientes | Plomo y arranque |
Esta diferencia es la razón por la que las transmisiones helicoidales alcanzan relaciones de 50:1 o más, algo imposible para un solo par de engranajes rectos.

Profundizar en el plomo y el ángulo del plomo
A diferencia de los engranajes rectos, que ruedan principalmente, los engranajes helicoidales funcionan con una acción deslizante única. Por eso son tan importantes el avance y el ángulo de avance. En PTSMAKE, nos centramos mucho en estos parámetros durante la fase de diseño.
¿Qué es el plomo?
El avance es la distancia axial que recorre la rosca helicoidal en una vuelta completa. No es lo mismo que paso.
Puedes calcular el plomo con esta sencilla fórmula:
Paso = Paso axial × Número de arranques
Un tornillo sin fin puede tener varias roscas, o "arranques". Más arranques significan un mayor avance y una menor relación de transmisión.
El papel del ángulo de ataque
El ángulo de avance es el ángulo entre la hélice de la rosca del tornillo sin fin y un plano perpendicular al eje del tornillo sin fin.
Un ángulo de avance pequeño (normalmente inferior a 10 grados) da lugar a una relación de transmisión elevada. Esta geometría también aumenta la fricción y la posibilidad de autobloqueo. Este movimiento crea velocidad de deslizamiento17que influye en la eficiencia y la elección del material.
Definición de ratios elevados
La combinación única de un pequeño avance y un tornillo sinfín de un solo arranque crea una reducción masiva de la velocidad. La relación de transmisión no depende solo del número de dientes, sino también de la geometría del tornillo sinfín.
| Arranques de gusano | Ángulo de ataque | Rango de relación típico |
|---|---|---|
| Único | Bajo | 40:1 a 100:1+ |
| Doble | Medio | 20:1 a 50:1 |
| Múltiples | Alta | 5:1 a 30:1 |
Como puede ver, el número de arrancadas influye directamente en el ángulo de avance y en la relación de transmisión resultante.
El paso y el ángulo de paso son los parámetros que definen los engranajes helicoidales. Sustituyen al concepto de paso utilizado en los engranajes rectos y son directamente responsables de los elevados ratios de reducción y del movimiento deslizante único característico de los engranajes helicoidales.
¿Cuál es la interacción entre la anchura de la cara y la capacidad de carga?
A primera vista, la lógica parece sencilla. Un engranaje más ancho debería soportar más carga. Esto suele ser cierto. Proporciona una mayor superficie de contacto para que los dientes engranen.
Sin embargo, este no es el cuadro completo. La relación es más compleja. Una mayor anchura de cara introduce nuevos retos que pueden afectar al rendimiento y la vida útil de los engranajes.
La espada de doble filo
Una cara más ancha aumenta la capacidad de carga teórica. Pero también hace que el sistema de engranajes sea mucho más sensible a cualquier desalineación. Incluso los errores más pequeños pueden causar problemas importantes.
| Aspecto | Cara más ancha | Ancho de cara más estrecho |
|---|---|---|
| Capacidad de carga | Más alto | Baja |
| Desalineación | Más sensible | Menos sensible |
| Distribución de la carga | Propenso a los desniveles | Más uniforme |
| Fabricación | Se necesitan tolerancias más estrictas | Más indulgente |
Esta sensibilidad puede anular las ventajas de un diseño más ancho.

El papel fundamental de la alineación
La alineación perfecta es poco frecuente en aplicaciones reales. La desviación del eje, el desgaste de los rodamientos y las tolerancias del alojamiento contribuyen a que se produzcan pequeñas desalineaciones.
Con una gran anchura de cara, estos pequeños errores hacen que la carga se concentre en un borde del diente. Esto crea puntos de presión intensa en lugar de distribuir la carga uniformemente por toda la cara. Esta desigualdad concentración de carga18 provoca un desgaste prematuro, picaduras e incluso la rotura de los dientes.
Encontrar el equilibrio: Relación entre anchura y diámetro de la cara
Para gestionar este equilibrio, los ingenieros utilizan la relación entre la anchura de la cara y el diámetro. Esta relación sirve de guía para diseñar engranajes estables y fiables. Cuando los clientes nos preguntan: "¿Los parámetros de los engranajes determinan el rendimiento?
En PTSMAKE trabajamos con nuestros clientes para encontrar el equilibrio óptimo. Nuestro mecanizado de precisión garantiza el mantenimiento de la alineación y la exactitud del perfil, maximizando las ventajas de la anchura de cara elegida.
Una regla empírica común es mantener esta relación dentro de un determinado rango para garantizar una buena distribución de la carga.
| Tipo de engranaje | Relación típica (anchura de la cara / diámetro del paso) |
|---|---|
| Engranajes rectos | 0,8 a 1,2 |
| Engranajes helicoidales | Hasta 2,0 |
| Engranajes cónicos | ~0,3 (de la distancia del cono) |
Seguir estas pautas ayuda a prevenir los efectos negativos de la desalineación.
Una mayor anchura de cara puede aumentar la capacidad de carga, pero exige una mayor precisión. Aumenta la sensibilidad a la desalineación, lo que puede provocar una distribución desigual de la carga y un fallo prematuro. La relación entre la anchura y el diámetro de las caras es una directriz de diseño crucial para el equilibrio.
¿Cómo interactúa el desplazamiento del perfil con la distancia entre ejes y la holgura?
El cambio de perfil es algo más que un concepto teórico. Es una poderosa herramienta que utilizamos en el diseño práctico de engranajes. Vincula directamente la geometría del diente con el montaje final.
Este ajuste nos permite resolver problemas de ingeniería del mundo real. Podemos modificar la forma en que los engranajes encajan y funcionan juntos.
La relación básica
Una aplicación clave es el ajuste de la distancia entre ejes. Un desplazamiento total positivo separa más las marchas. Un desplazamiento total negativo las acerca. Este principio es fundamental.
| Tipo de turno | Efecto sobre la distancia entre ejes |
|---|---|
| Positivo | Aumenta |
| Negativo | Disminuye |
| Cero | Estándar |
Este control es vital para las aplicaciones personalizadas.

En el diseño de engranajes, saber cuáles son sus parámetros es crucial. El desplazamiento de perfil es uno de estos parámetros más versátiles. Proporciona una solución elegante para distancias de montaje no estándar.
Adaptarse a las limitaciones del mundo real
Imagínese que necesita montar engranajes en una carcasa ya existente. Los puntos de montaje son fijos y no están a una distancia estándar. En este caso, el cambio de perfil es esencial.
Aplicando un desplazamiento positivo o negativo calculado, modificamos los engranajes. Esto permite que engranen perfectamente a esa distancia específica, no estándar. En PTSMAKE utilizamos a menudo esta técnica para las piezas de recambio.
Este método evita rediseñar conjuntos enteros. Ahorra tiempo y costes significativos a nuestros clientes.
Ajuste de la holgura
El desplazamiento del perfil también es mi método preferido para controlar la holgura. Un desplazamiento positivo aumenta el diámetro de paso operativo. Esta acción aumenta naturalmente el espacio, o juego, entre los dientes engranados.
A la inversa, un desplazamiento negativo lo reduce. Esta precisión es fundamental en aplicaciones que requieren un juego mínimo. El sitio adenda modificación coeficiente19 es el factor que ajustamos para conseguirlo.
La relación puede resumirse del siguiente modo:
| Desplazamiento total del perfil | Distancia al centro | Contragolpe |
|---|---|---|
| Positivo | Aumenta | Aumenta |
| Negativo | Disminuye | Disminuye |
Según los resultados de nuestras pruebas, esta capacidad de ajuste fino es indispensable para los sistemas de alta precisión. Garantiza un rendimiento óptimo y un menor desgaste con el paso del tiempo.
El desplazamiento de perfil es una herramienta práctica para ajustar conjuntos de engranajes. Modifica directamente la distancia entre ejes y permite un control preciso de la holgura, resolviendo problemas habituales con montajes no estándar y requisitos de rendimiento.
¿Cuál es el sistema de grados de precisión de los engranajes (por ejemplo, ISO, AGMA)?
Los grados de precisión de los engranajes son un sistema de clasificación fundamental. Clasifican los engranajes en función de su precisión de fabricación. Esto garantiza una calidad y un rendimiento uniformes en diferentes lotes.
Estas normas, como ISO 1328 y AGMA 2015, no son arbitrarias. Definen errores específicos permitidos para parámetros críticos de los engranajes.
Por ejemplo, fijan límites a la desviación de paso y al error de perfil. La elección del grado es crucial. Viene determinada por factores como la velocidad de funcionamiento y los niveles de ruido aceptables para la aplicación final.

La idea central es sencilla. Un número de grado inferior, como ISO 4 o AGMA Q13, significa mayor precisión. Un número superior, como ISO 12 o AGMA Q6, indica un nivel de precisión inferior.
Esta precisión se mide en función de tolerancias geométricas específicas. Las normas proporcionan gráficos detallados que definen cuáles son los parámetros de un engranaje y sus límites aceptables para cada grado de precisión.
He aquí algunos parámetros clave controlados por estas normas:
| Parámetro | Descripción | Impacto en el rendimiento |
|---|---|---|
| Desviación de la inclinación | El error en la distancia entre dientes adyacentes. | Afecta a la suavidad de funcionamiento y a los niveles de ruido. |
| Error de perfil | La desviación de la forma ideal del diente involuto. | Influye en los patrones de desgaste y en la distribución de la carga. |
| Desviación de la hélice | El error en el ángulo del trazado del diente del engranaje. | Afecta al contacto de los dientes y a la capacidad de carga global. |
| Runout | La excentricidad de los dientes del engranaje con respecto a su eje. | Provoca vibraciones y puede provocar un desgaste desigual. |
Elegir la calidad adecuada es una decisión de diseño fundamental. Las aplicaciones de alta velocidad, como las de las transmisiones de automoción o la robótica, exigen grados de alta precisión. Esto minimiza las vibraciones, el ruido y el desgaste prematuro. Una ligera desviación de cabeceo acumulada20 puede causar problemas significativos a altas RPM.
En cambio, un mecanismo no crítico de baja velocidad, como una manivela manual, puede funcionar perfectamente con una calidad inferior y más económica. En PTSMAKE, guiamos a nuestros clientes en la selección del grado óptimo para equilibrar los requisitos de rendimiento con su presupuesto.
Los grados de precisión de los engranajes clasifican la precisión de fabricación estableciendo tolerancias para parámetros como el error de paso y de perfil. El grado adecuado viene determinado por las necesidades específicas de la aplicación, principalmente sus limitaciones de velocidad de funcionamiento, carga y ruido, garantizando un rendimiento y una rentabilidad óptimos.
¿Cómo se selecciona el módulo inicial de un nuevo diseño?
Elegir el módulo inicial adecuado es un primer paso fundamental. Influye directamente en la resistencia, el tamaño y el rendimiento general del engranaje. Un módulo demasiado pequeño fallará. Uno demasiado grande añade peso y costes innecesarios.
El núcleo del proceso es un equilibrio. Debe sopesar el par necesario y la resistencia del material. Este cálculo inicial proporciona una base sólida para todo el diseño del engranaje. Ayuda a evitar costosos rediseños posteriores.
Una metodología práctica
El proceso comienza con los parámetros clave del engranaje: par y resistencia del material. Estas cifras son el punto de partida para todo lo demás.
| Paso | Acción | Propósito |
|---|---|---|
| 1 | Definir el par | Conozca la carga máxima que puede soportar el equipo. |
| 2 | Seleccionar material | Elija en función de la resistencia, el desgaste y el coste. |
| 3 | Calcular el estrés | Determine la resistencia necesaria del diente. |
| 4 | Normalizar | Seleccione el módulo estándar más cercano. |
Este enfoque sistemático garantiza que su equipo pueda realizar su trabajo sin fallar.

Sumergirse en el cálculo
Un método práctico comienza con cálculos preliminares de tensiones. En PTSMAKE, solemos empezar con fórmulas como las de Lewis o AGMA. Estas ayudan a estimar las fuerzas que actúan sobre un solo diente de engranaje.
Análisis de esfuerzos de flexión
En primer lugar, analizamos el esfuerzo de flexión. Este cálculo determina si un diente se romperá por su raíz bajo carga. Se utilizan el par y la geometría del engranaje como datos de entrada. El resultado indica el tamaño mínimo que debe tener el diente. Así se obtiene un valor preliminar del módulo.
Análisis de la tensión de contacto
A continuación, examinamos la durabilidad de la superficie. La fuerza entre los dientes engranados puede provocar picaduras o desgaste con el paso del tiempo. El análisis de tensión de contacto21 es crucial para los engranajes que deben durar mucho tiempo. Garantiza que la superficie del diente no se deforme ni falle prematuramente.
Del cálculo a la normalización
Estos cálculos le dan un módulo necesario, como 2,37 mm. Sin embargo, no es fácil fabricar un módulo a medida de 2,37 mm. Hay que redondearlo al valor estándar más próximo, como 2,5 mm.
| Módulo calculado | Elección del módulo estándar | Razón |
|---|---|---|
| 1,15 mm | 1,25 mm | Redondea al alza para tener un margen de seguridad. |
| 2,37 mm | 2,50 mm | Norma de fabricabilidad. |
| 3,89 mm | 4,00 mm | Garantiza la resistencia y la disponibilidad. |
Elegir un módulo estándar simplifica la fabricación y reduce los costes. Garantiza que pueda abastecerse fácilmente de herramientas de corte y calibres de inspección. Se trata de un paso clave en nuestro proceso de diseño para la fabricación.
Para seleccionar un módulo inicial, comience con el par y la resistencia del material. Realice cálculos preliminares de tensión para encontrar un módulo necesario. Por último, redondee este valor al módulo estándar más cercano para garantizar la fabricabilidad y fiabilidad de su diseño.
¿Cómo elegir entre un ángulo de presión estándar y uno mayor?
Elegir el ángulo de presión de tu equipo parece una decisión importante. Pero es más sencillo de lo que crees. La mayoría de las veces, el ángulo estándar de 20° es la elección perfecta. Ofrece un gran equilibrio de rendimiento.
Sin embargo, algunos diseños necesitan más. Si debe maximizar el par en un espacio reducido, es mejor un ángulo mayor. Éste es un reto habitual cuando se consideran todos los parámetros del engranaje (Parámetros del engranaje). Veamos un marco sencillo.
| Ángulo de presión | Uso principal | Compromiso clave |
|---|---|---|
| 20° (Estándar) | Aplicaciones generales | Rendimiento equilibrado |
| 25° (Más grande) | Alto par, diseños compactos | Aumento del ruido |
Piense que 20° es su ajuste por defecto. Cámbialo solo si tienes una razón específica y convincente.

Profundizar en la decisión
Veamos el "por qué" de esta elección. El ángulo de presión influye directamente en la forma del diente del engranaje. Un ángulo de presión mayor, como 25°, da como resultado un diente más ancho y más corto.
Dientes más fuertes, mayor capacidad
Esta base más ancha hace que el diente sea intrínsecamente más fuerte. Puede soportar más fuerza sin romperse. Por eso es ideal para aplicaciones que exigen una alta transmisión de par. En proyectos anteriores de PTSMAKE, hemos utilizado ángulos de 25° para brazos robóticos de gran resistencia.
Un ángulo mayor también ayuda a prevenir un problema común. Reduce el riesgo de subcotización22 en engranajes con un número reducido de dientes, lo que puede debilitar el engranaje.
Las contrapartidas
Pero esta resistencia tiene un coste. Un mayor ángulo de presión aumenta la carga radial sobre los rodamientos. Los rodamientos deben ser lo suficientemente robustos como para soportar esta fuerza adicional. También puede dar lugar a una relación de contacto ligeramente inferior, lo que puede provocar más ruido de funcionamiento.
He aquí una comparación más detallada:
| Característica | Ángulo de presión de 20 | Ángulo de presión de 25 |
|---|---|---|
| Capacidad de par | Bien | Excelente |
| Resistencia dental | Estándar | Más alto |
| Carga portante | Baja | Más alto |
| Nivel de ruido | Más silencioso | Potencialmente más ruidoso |
| Ratio de contacto | Más alto | Baja |
Su elección depende de cuáles de estos factores son más críticos para su aplicación específica.
En resumen, el ángulo de presión de 20° es la norma del sector por una buena razón. Opte por un ángulo mayor de 25° solo cuando la necesidad de una mayor capacidad de par y resistencia del diente en un espacio compacto supere el potencial de aumento del ruido y las cargas sobre los rodamientos.
¿Cómo se optimizan los parámetros de los engranajes para reducir el ruido de la transmisión?
Reducir el ruido de los engranajes no es una fórmula mágica. Se trata de combinar varios parámetros del engranaje. Cada uno de ellos desempeña un papel.
Un diseño silencioso de éxito integra estos elementos. Es un enfoque holístico que utilizamos a menudo en PTSMAKE para nuestros clientes.
Alta relación de contacto
Una mayor relación de contacto significa que se engranan más dientes a la vez. Esto distribuye la carga y suaviza la transferencia de potencia. A menudo lo conseguimos con engranajes helicoidales.
Grado de precisión
La precisión no es negociable para un funcionamiento silencioso. Un grado de precisión más alto, como ISO 5 o superior, garantiza que los dientes engranen perfectamente. Esto reduce los impactos y las vibraciones.
Modificaciones del perfil de los dientes
Incluso con una gran precisión, las modificaciones son fundamentales. El abombamiento y el alivio de la punta compensan las desalineaciones y desviaciones bajo carga.
| Parámetro | Objetivo principal de la reducción del ruido |
|---|---|
| Ratio de contacto | Transferencia de potencia suave, distribución de la carga |
| Grado de precisión | Minimizar los impactos y las vibraciones |
| Modificación del perfil | Compensación de las desviaciones reales |

Un juego de engranajes realmente optimizado sinergiza múltiples parámetros. No basta con seleccionar un grado de precisión elevado. En proyectos anteriores, hemos visto cómo engranajes muy precisos no superaban las pruebas de ruido. Esto ocurre cuando no tienen en cuenta la deflexión del eje bajo carga.
El papel de las modificaciones dentales
Aquí es donde brillan las modificaciones del perfil de los dientes.
Coronación y relieve de la punta
El coronado curva ligeramente la cara del diente. Esto evita que los bordes del diente se claven cuando el eje se dobla. El alivio de la punta elimina una pequeña cantidad de material en la punta del diente. Facilita la entrada y salida del diente de la malla. Estas modificaciones son cruciales para minimizar Error de transmisión23.
Combinar parámetros para el éxito
A menudo utilizamos engranajes helicoidales. Naturalmente, tienen una elevada relación de contacto. A continuación, especificamos un grado de alta precisión. Por último, aplicamos modificaciones precisas del perfil del diente.
Según nuestras pruebas, esta combinación es increíblemente eficaz. Garantiza una acción de engrane suave y continua.
El cuadro siguiente muestra una comparación simplificada.
| Tipo de engranaje | Relación de contacto típica | Nivel de ruido | Modificaciones comunes |
|---|---|---|---|
| Espolón estándar | 1.2 - 1.6 | Moderado | Alivio de puntas |
| Helicoidal | > 2.0 | Bajo | Coronación y alivio de la punta |
Esta estrategia integrada garantiza un funcionamiento silencioso de los engranajes. También son más duraderos, ya que se minimizan las concentraciones de tensiones. Este es un principio básico de nuestros servicios de mecanizado y moldeado CNC.
Conseguir engranajes silenciosos requiere un enfoque holístico. Se trata de combinar relaciones de contacto elevadas, una fabricación precisa y modificaciones específicas de los dientes. Estos elementos deben trabajar juntos para minimizar las vibraciones en su origen.
¿Cómo cambian los parámetros de los engranajes cuando se diseña para plástico frente a acero?
Cuando se pasa del acero al plástico para el diseño de engranajes, no se puede utilizar el mismo plano. Las propiedades de los materiales son fundamentalmente distintas. Esto requiere cambios significativos en los parámetros clave del engranaje.
Debemos ajustar el diseño para compensar la menor resistencia del plástico y su mayor dilatación térmica. Analicemos los cambios más importantes.
Ajustes de parámetros clave
Es esencial saber qué parámetros del engranaje hay que ajustar. Los principales son el módulo, el ángulo de presión y el juego. Cada uno de ellos contribuye a garantizar un funcionamiento fiable del engranaje.
| Parámetro | Diseño de engranajes de acero | Diseño de engranajes de plástico |
|---|---|---|
| Módulo | Normalmente más pequeños | Necesita ser más grande |
| Ángulo de presión | Estándar (por ejemplo, 20°) | A menudo más grandes (por ejemplo, 25°) |
| Contragolpe | Tolerancia más estricta | Requiere más espacio libre |

Por qué los engranajes de plástico necesitan parámetros diferentes
La razón principal de estos cambios radica en las propiedades físicas del material. El plástico no es tan resistente ni estable como el acero.
Módulo más grande para mayor resistencia
El plástico tiene una resistencia a la tracción mucho menor que el acero. Para compensarlo, aumentamos el módulo del engranaje. Un módulo mayor se traduce en dientes más grandes y gruesos.
Estos dientes más grandes pueden soportar más tensión. Distribuyen la carga sobre un área más amplia, evitando fallos prematuros. Se trata de una solución sencilla pero eficaz.
Mayor ángulo de presión
También ayuda un mayor ángulo de presión, a menudo de 25° en lugar de los 20° estándar. Crea una base dentaria más ancha y fuerte. Este diseño reduce el riesgo de que los dientes se doblen o se rompan bajo carga. Es un ajuste habitual que realizamos en PTSMAKE para sistemas de engranajes de plástico robustos.
Mayor rechazo a la ampliación
Los plásticos se dilatan y contraen considerablemente con los cambios de temperatura. También pueden hincharse en ambientes húmedos debido a expansión higroscópica24. Esta inestabilidad dimensional es motivo de gran preocupación.
Diseñamos engranajes de plástico con más holgura. Esta holgura adicional garantiza que los engranajes no se atasquen al expandirse. Sin ella, el sistema fallaría.
| Cambio de parámetros | Razón de ser de los engranajes de plástico |
|---|---|
| Módulo más grande | Compensa la menor resistencia del material. |
| Mayor ángulo de presión | Crea una base dental más ancha y fuerte. |
| Aumento del contragolpe | Se adapta a la dilatación térmica y a la humedad. |
Diseñar con plástico requiere ajustar los parámetros clave del engranaje. Un módulo más grande y un ángulo de presión añaden resistencia, mientras que un mayor juego evita los atascos provocados por la dilatación térmica o la humedad. Estos cambios son cruciales para conseguir un sistema de engranajes fiable.
¿Cómo se crea una lista de comprobación personal para revisar los parámetros de diseño de los equipos?
Una lista de comprobación personal es su mejor defensa contra errores costosos. Transforma la teoría en un proceso práctico y repetible. Esta herramienta le garantiza que nunca pasará por alto detalles críticos.
Pasar del CAD a una pieza física requiere una revisión sistemática. Qué parámetros del engranaje debe comprobar primero?
Geometría fundamental
Empieza por lo básico. Estos parámetros definen la forma y la interacción del engranaje. Confirme el número de dientes, el módulo y el ángulo de presión.
Resistencia y material
A continuación, verifique la resistencia. Asegúrese de que el material elegido y el tratamiento térmico pueden soportar los ciclos de torsión y tensión previstos. Así se evitan fallos prematuros.
| Categoría de parámetros | Puntos clave que hay que comprobar |
|---|---|
| Geometría | Módulo, ángulo de presión, número de dientes |
| Fuerza | Selección de material, dureza, filete de raíz |

Revisión de la fabricabilidad
Un diseño perfecto no sirve de nada si no se puede fabricar. En PTSMAKE, a menudo vemos diseños difíciles o caros de producir.
Su lista de comprobación debe incluir una puerta de fabricabilidad. ¿Puede cortarse el perfil del diente con herramientas estándar? ¿Hay rebajes que requieran procesos especializados? Unos sencillos ajustes pueden reducir considerablemente los costes.
Montaje y aplicación
Piense en cómo encaja el engranaje en el sistema general. La distancia entre ejes de los engranajes es crucial. Tenga en cuenta también contragolpe25 para un funcionamiento correcto.
Por último, revise las necesidades específicas de la aplicación. ¿Necesita el sistema poco ruido? Esto puede influir en la elección del ángulo de hélice o el acabado superficial. ¿Cuál es la vida útil prevista? Esto afecta a la elección del material y la lubricación.
Una minuciosa lista de comprobación une la intención del diseño con el rendimiento en el mundo real.
| Área de revisión | Consideraciones clave | Impacto |
|---|---|---|
| Fabricabilidad | Recortes, acceso a herramientas, tolerancias | Coste de producción y plazo de entrega |
| Montaje | Distancia entre centros, comprobaciones de interferencias | Funcionalidad y ajuste del sistema |
| Aplicación | Ruido (NVH), vida útil, lubricación | Rendimiento y fiabilidad del producto final |
Una exhaustiva lista de comprobación garantiza la revisión de todos los parámetros críticos. Este enfoque metódico minimiza los errores, agiliza la producción y garantiza que el engranaje final funcione exactamente según lo previsto en su aplicación.
Desbloquee la experiencia en engranajes con PTSMAKE, su socio de engranajes de precisión
¿Necesita soluciones de engranajes fiables y de precisión adaptadas a sus requisitos específicos? Póngase en contacto con PTSMAKE hoy mismo para obtener un presupuesto competitivo de componentes de engranajes mecanizados por CNC o moldeados por inyección. Nuestro equipo suministra rápidamente piezas personalizadas de alta calidad y asesoramiento experto, agilizando su proyecto desde el prototipo hasta la producción. Envíenos su petición de oferta ahora.
Descubra cómo este círculo imaginario constituye la base de todos los cálculos geométricos de engranajes críticos. ↩
Aprenda cómo interactúan los dientes de los engranajes para garantizar una transmisión de potencia suave y eficaz en sus diseños. ↩
Explore este concepto para comprender mejor cómo se transmite la fuerza entre los dientes de un engranaje. ↩
Aprenda cómo esta colisión de dientes de engranaje puede causar un fallo catastrófico y cómo evitarlo. ↩
Vea cómo este problema puede causar fallos en el sistema y aprenda las mejores prácticas para evitarlo. ↩
Explore la curva geométrica que garantiza una velocidad constante y una transmisión suave de la potencia en los engranajes. ↩
Descubra por qué los diámetros de paso son los círculos teóricos que definen cómo ruedan los engranajes y transmiten el movimiento. ↩
Comprender los principios de cálculo de la tensión en el punto de contacto entre dos cuerpos curvos. ↩
Conozca la curva evolvente, la base geométrica de la mayoría de los dentados modernos y cómo se ve afectada por las modificaciones. ↩
Descubra cómo afecta la concentración de tensiones a la durabilidad de las piezas y nuestros métodos para mitigarla. ↩
Descubra cómo influye esta fuerza en la elección de los rodamientos y en el diseño general del sistema. ↩
Haga clic para comprender esta dimensión crucial del engranaje y su impacto en el rendimiento de su diseño. ↩
Descubra cómo la socavación puede debilitar los dientes de los engranajes y por qué es crucial evitarla en la fabricación de engranajes. ↩
Conozca los detalles técnicos de cómo este ajuste optimiza el rendimiento y la resistencia del engranaje. ↩
Descubra cómo se descompone la fuerza total en componentes para mejorar el análisis del diseño mecánico. ↩
Obtenga más información sobre este factor geométrico crucial que define la duración del engranaje. ↩
Descubra cómo influye este factor en la eficacia, las necesidades de lubricación y la elección de materiales en el diseño de engranajes. ↩
Aprenda a calcular y mitigar los riesgos de los puntos de alta tensión en los dientes de los engranajes. ↩
Descubra cómo este parámetro clave redefine la geometría y el rendimiento de los engranajes. ↩
Descubra cómo afecta este parámetro crítico al rendimiento del tren de engranajes y a la precisión posicional. ↩
Comprender cómo la presión superficial entre engranajes influye en la durabilidad y la vida útil. ↩
Aprenda qué es la socavación y cómo un mayor ángulo de presión puede evitarla eficazmente. ↩
Descubra cómo esta métrica clave cuantifica la precisión de engrane de los engranajes y su impacto directo en el ruido. ↩
Sepa cómo afecta la absorción de humedad al tamaño y rendimiento de sus engranajes de plástico. ↩
Descubra cómo influye este pequeño espacio en el ruido de los engranajes, el desgaste y la eficacia general del sistema. ↩








